Dead Weight Loss
Accidentally I stumbled upon a disparity between the definition of Harberger’s triangle or deadweight loss as it is employed in a Dutch textbook I consulted as opposed to the way it is employed in my son’s A-level textbook or the IB textbook in our possession.
Harberger’s triangle as measured on a supply and demand graph is generally attributed to American economist Arnold Harberger. It shows the deadweight loss associated with government intervention in a perfect market. Mechanisms for this intervention include price floors, caps, taxes, tariffs, or quotas. It also refers to the deadweight loss created by a government’s failure to intervene in a market with externalities, or the loss resulting from imperfect competition. Regretfully, I did not read this myself in a paper published by Harberger himself in, say, 1951, but I had to turn to Wikipedia as my source. Note that deadweight loss has government failure written all over it. Notice too, that externalities and imperfect competition, like monopolies, are both branches of the same tree, that is market failure.
The Dutch textbook I consulted, adheres to the application of Harberger’s triangle in a market with perfect competition, where government intervention leads to welfare loss. Straightforward, but not very interesting, since there aren’t many examples of markets with perfect competition in real life. Instead of giving the black mark to the government, the authors could consider applying Harberger’s triangle to monopolies or market power in general, as stated in the economics guide.
In the UK, it seems exam boards lean towards deadweight loss as a result of market failure in general. In this respect externalities make for the most interesting case, since they put government intervention in perspective. Interventions, like taxation, price floors or caps, and subsidies are in general aimed at correcting market failure due to externalities.
The textbook I consulted reasoned as follows:
Assume a market for good A, represented by the diagram below, where the green line represents demand, and the blue line supply:
The market equilibrium is marked with an A, with quantity 0C and price 0B. The consumer surplus is designated with the green triangle and the producer surplus with the blue triangle.
Now assume the government intervenes in this market through an indirect tax. This causes the supply line to shift to the left and up, effectively causing an increase in price at every quantity supplied and bought:
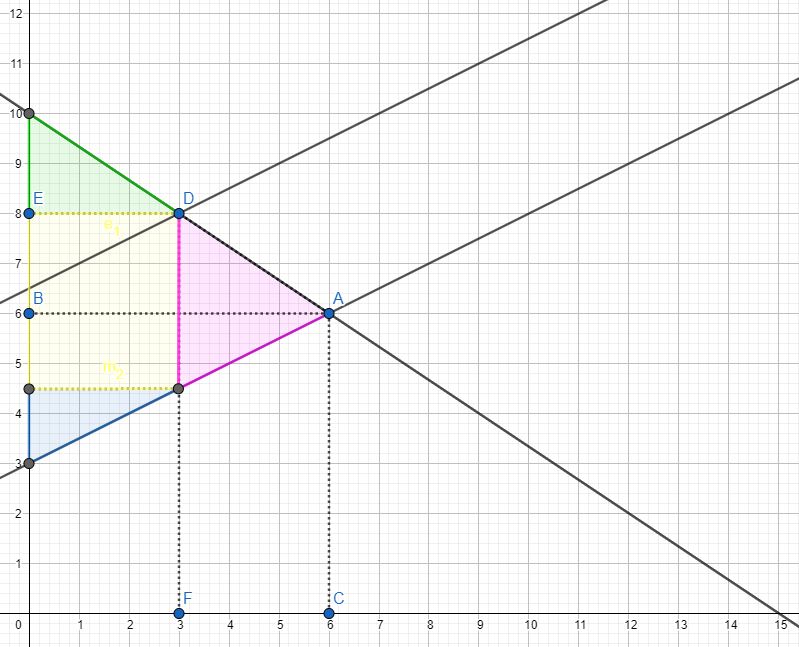
The result is a new market equilibrium marked with D, with quantity 0F and price 0E. The amount of tax is designated by the pink vertical line. Since the price has increased from 0B to 0E, buyers pay (0E – 0B) of tax per unit and the remainder is covered by the supplier. Total tax revenue for the government is shown with the yellow rectangle. Both surplus are again marked in green and blue.
Tax revenue and the sum of the consumer and producer surplus add up to a total that is lower than before taxation to the amount of the pink triangle, the Harberger’s triangle or deadweight loss.
This is where the analysis is concluded in the Dutch textbook I consulted, leaving students under the impression that government intervention leads to welfare loss.
The British, however, come to a different conclusion with respect to deadweight loss. They, in a sense, take a step back. The question is why the government deemed it necessary to intervene. Did it intend to increase public revenue, or did it intend to mitigate externalities? To analyse this, the British textbooks introduce the concept of social cost and benefits, which is the sum total of public and private cost and benefits. To illustrate this I will continue the taxation example, but take it one step back to the intention the government has with this intervention: to decrease the quantity consumed and produced. I will continue to call the product good A, but you can call it petrol if you like.
Demand is now labeled with MPB, marginal private benefit, and MSB, marginal social benefit. In this example we assume these to be equal. Supply is labeled with MPC, marginal private cost. I have drawn a new line to indicate the MSC, or marginal social cost.
At the original equilibrium A MPB and MPC are equal, with price 0B and quantity 0C. At this quantity level the marginal public cost, the public cost for one unit of good A are (IC – AC).
Point E is the preferred market outcome, since in this point MSB equals MSC.
Notice that the consumer and producer surplus are the same as before taxation. This level of consumption and production comes with a cost, however, illustrated with the red quadrilateral.
Part of the quadrilateral is covered by the market surplus, and it seems that one man’s gain is another man’s loss is acceptable, because only the triangle IFA is seen as a welfare loss, or a deadweight loss:
In the British textbooks we have consulted the analysis does not go any further. These texts do not go into the trade off between private benefits and public costs or the distribution of the surplus. I want to take it one step further, effectively combining the Dutch’ and British’ textbook analysis, by bringing taxation back into the equation:
To reach the preferred market equilibrium E, the government levies a tax EH, which results in the orange line, MPC with tax. The consumer price increases to 0G, with quantity 0F.
The distribution of the surplus across consumers, producers and tax revenue should be familiar, since it is the same as in the Dutch analysis of government intervention. The interpretation of the ‘loss’ is however different:
There is no deadweight loss anymore, but instead a substantial welfare gain, illustrated with the pink quadrilateral. This consists of the deadweight loss (triangle FAJ) and a public surplus that was previously a private surplus (triangle FHA), thus the trade off between the public and private surplus has been reversed to the extent of triangle FHA. Part of the original trade off between public cost and private surplus still exists, designated with the red quadrilateral. However, in this situation the government could use its tax revenue to offset the public cost:
I find this difference in approach rather interesting. It comes across like the difference in the glass half full / glass half empty perspectives. I leave it to you to decide which is which.
henny@21steconomics.org – You can also find me on LinkedIn







